티스토리 뷰
베르누이 시행
결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행(Bernoulli trial)이라고합니다. 예를 들어 동전을 한번 던져 앞면이 나오거나 뒷면이 나오게 하는 것도 베르누이 시행입니다.
베르누이 확률변수
베르누이 시행의 결과를 실수 0 또는 1로 바꾼 것을 베르누이 확률변수(Bernoulli random variable)라고 ㅎ바니다. 베르누이 확률변수는 두 값 중 하나만 가질 수 있으므로 이산확률 변수(discrete random variable)입니다. 베르누이 확률변수의 표본값은 보통 정수 1과 0으로 표현하지만 때로는 정수 1과 -1로 표현하는 경우도 있습니다.
베르누이 분포(Bernoulli Distribution)

이항분포의 정의는 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질때의 이산 확률 분포입니다. 여기서 n = 1일때 이항분포는 베르누이 분포입니다.
베르누이 확률변수의 분포를 베르누이 확률분포 혹은 베르누이분포라고 합니다. 확률 이론 및 통계학에서 주로 사용되는 이론으로, 스위스의 수학자 야코프 베르누이의 이름에 따라 명명되었습니다. 베르누이 분포는 확률론과 통계학에서 매 시행마다 오직 두가지의 간으한 결과만 일어난다고 할 때, 이런한 실험을 1회 시행하여 일어난 두가지 결과에 대해 그 값이 각각 0과 1로 결정되는 확률변수 X에 대해서 위의 식을 만족하는 확률변수 X가 따르는 확률분포를 의마하며, 이항 분포의 특수한 사례에 속합니다.
만약 어떤 확률변수 X가 베르누이분포에 의해 발생된다면 '확률변수 X가 베르누이 분포를 따른다'라고 말하고 다음과 같이 수식으로 씁니다.

베르누이 분포의 확률질량함수 수식은 다음과 같습니다.

베르누이분포는 1이 나올확률을 의미하는 µ라는 모수(parameter)를 가집니다. 변수와 모수는 세미콜론 기호로 분리했습니다. 0이 나올 확률은 1 - µ 입니다.
위 식을 하나의 수식으로 표현하면 다음처럼 쓸 수 있습니다.
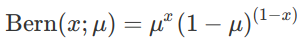
베르누이 확률변수의 평균과 분산
