티스토리 뷰
문제 : https://programmers.co.kr/learn/courses/30/lessons/1833
코딩테스트 연습 - 캠핑 | 프로그래머스
캠핑 무지를 돌보느라 지친 콘은 한적한 시골의 한 캠핑장에 놀러 갔다. 캠핑장은 텐트를 칠 수 있는 넓은 평지를 제공하고 있는데, 이 평지에는 이미 캠핑장에서 설치해 놓은 n개의 쐐기가 박혀 있다. 캠핑장 이용 고객은 이 쐐기들 중 한 쌍을 골라 다음과 같은 조건을 만족하도록 텐트를 설치해야 한다. 텐트는 직사각형 형태여야 한다. 텐트의 네 면이 정확하게 동, 서, 남, 북을 향해야 한다. 대각에 위치하는 텐트의 두 꼭짓점이 정확하게 선택한 두 개의 쐐기
programmers.co.kr
주어진쐐기들 중 2가지를 고르는 것이 기본적인 풀이 방법이라 생각되어 진행하였습니다. O(N^2)
입력 값의 변형, 쐐기들끼리 선 긋기, 기울기를 이용한 풀이...여러가지를 생각하였지만 기존의 내 생각으론 풀 수 없었습니다.
먼저 해답을 보니 'Prefix sum'에 대해 설명하고 있었습니다.
그런데 어느 블로그에는 'segment tree'를 이용한 풀이라고 설명하고 있습니다.
둘다 처음엔 뭔가 했지만 하나씩 찾아보고 이해하였고, 자세한건 알고리즘 개념 메뉴에서 위의 두 개념에 대해 설명하고 있습니다.
다시 문제로 돌아가서 'Prefix sum'을 사용하여 구하고자 하는 구역에 쐐기가 있는지 판단합니다.
1. 주어진 범위의 직사각형 내부에 쐐기가 몇개 있는지를 먼저 구해놓는다 -> O(N^2)
S[i][j] : (0, 0) ~ (i, j) 범위의 직사각형 내부에 존재하는 쐐기의 개수
2. 그리고 모든 쐐기의 쌍에 대하여 -> O(N^2)
미리 구해놓은 S 배열의 값을 검사하여
값이 0인 경우 (내부에 쐐기가 없음) 텐트를 설치할 수 있음을 쉽게 판단할 수 있게됩니다.
그림 출처 : https://jaejin0me.github.io/post/algo46/
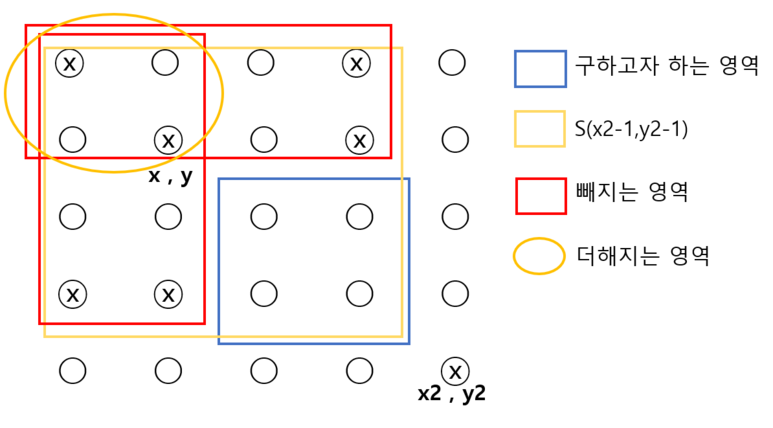
(x, y)와 (x2, y2)를 내부쐐기로 선정한다고 하였을때, 내부 쐐기 = S[x2-1][y2-1] - S[x2-1][y] - S[x][y2-1] + S[x][y] 이다.
구하고자 하는 것이 파란박스임을 생각한다면 도출될 수 있는 결론입니다.
위의 식을 실행하기 전에 우선 좌표압축을 실시합니다
좌표압축은 좌표들의 값들이 각각 특정한 의미를 지닌다기보다는, 위치의 순서를 나타낼때 사용하기 좋습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
int S[5000][5000]; //내부 쐐기의 개수 저장 배열
void location_compression(int n, vector<vector<int>>& data) {
vector<int> xpoints; // x좌표 집합
vector<int> ypoints; // y좌표 집합
for (int i = 0; i < data.size(); i++) { //데이터에 있는 좌표를 x,y로 나누어 넣음
xpoints.push_back(data[i][0]);
ypoints.push_back(data[i][1]);
}
unordered_set<int> uniqXpoints(xpoints.begin(), xpoints.end()); // 중복 값 제거를 위해 셋에 넣음
unordered_set<int> uniqYpoints(ypoints.begin(), ypoints.end());
xpoints.assign(uniqXpoints.begin(), uniqXpoints.end()); //중복제거된 값을 다시 넣기
ypoints.assign(uniqYpoints.begin(), uniqYpoints.end());
sort(xpoints.begin(), xpoints.end()); // 정렬
sort(ypoints.begin(), ypoints.end());
int x = 0, y = 0; //좌표 압축
for (int i = 0; i < data.size(); i++) {
for (int j = 0; j < xpoints.size(); j++) {
if (data[i][0] == xpoints[j]) {
x = j;
data[i][0] = x; // 좌표를 인덱스로 교체
break;
}
}
for (int k = 0; k < ypoints.size(); k++) {
if (data[i][1] == ypoints[k]) {
y = k;
data[i][1] = y; // 좌표를 인덱스로 교체
break;
}
}
S[x][y] = 1; // 쐐기가 있는 곳은 미리 1로 설정
}
return;
}
|
위의 과정으로 좌표 압축을 하고
|
1
2
3
4
5
6
7
8
9
10
11
12
|
// 각 영역별 쐐기 값을 누적으로 구하기
// 인덱스에 -1을 하므로, 범위에 벗어나지 않도록 주의한다.
// 차례대로 하는 이유가 있다!
void prefix_sum(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
S[i][j] += (i-1 > -1 ? S[i-1][j]:0) +(j-1> -1 ? S[i][j-1]:0)
- (i-1> -1 && j-1> -1 ? S[i-1][j-1]:0);
}
}
|
각 영역별 쐐기 값을 누적으로 구하였습니다. S행렬의 순서 없이 위 과정을 진행할 경우
저장한 값들이 꼬이는 경우가 발생합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
void processing(int n, vector<vector<int>>& data) {
int ans = 0;
int cnt = 0;
int startX, startY, endX, endY;
// 모든 쐐기에 대해 조사
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// 크기 1이상의 직사각형이 아닌경우
if (data[i][0] == data[j][0] || data[i][1] == data[j][1]) continue;
// 크기 1이상의 직사각형이 존재하는 경우
cnt = 0;
startX = data[i][0] < data[j][0] ? data[i][0] : data[j][0];
startY = data[i][1] < data[j][1] ? data[i][1] : data[j][1];
endX = data[i][0] > data[j][0] ? data[i][0] : data[j][0];
endY = data[i][1] > data[j][1] ? data[i][1] : data[j][1];
//내부의 공간이 1 인 경우, 쐐기가 있을 공간이 없음
if (startX + 1 > endX - 1 || startY + 1 > endY - 1) {
cnt = 0;
}
else {
//
cnt = S[endX - 1][endY - 1] - S[endX - 1][startY] - S[startX][endY - 1] + S[startX][startY];
}
if (cnt == 0) ans++; //내부에 존재하는 쐐기의 개수가 0이면 가능한 경우
}
}
return ans;
}
|
모든 쐐기에 대하여 텐트를 설치할 수 있는지 없는지 확인합니다.
확인하는 과정은 미리 계산해 놓은 prefix_sum 때문에 많은 시간이 걸리지 않습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
int solution(int n, vector<vector<int>> data) {
int answer = 0;
vector<vector<int>> mydata = data;
memset(S, 0, sizeof(S)); // 0으로 세팅
location_compression(n, mydata);
prefix_sum(n);
answer = processing(n, mydata);
return answer;
}
|
메인함수라고 보시면 됩니다.