티스토리 뷰
위상정렬(Topological Sort)
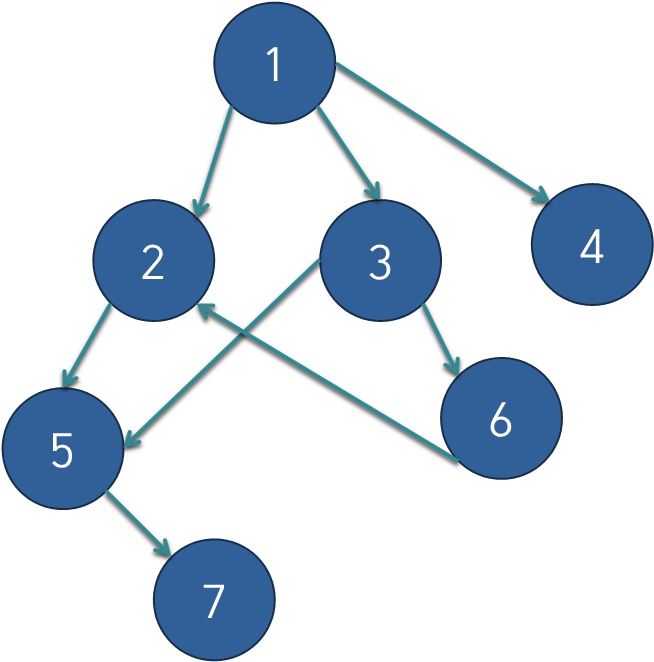
위상정렬(topological sorting)은 유향 그래프의 꼭짓점들(vertex)을 변의 방향을 거스르지 않도록 나열하는 것을 의미합니다. 위상정렬을 가장 잘 설명해 줄수 있는 예로 대학의 선수과목 구조를 들 수 있습니다. 만약 특정 수강과목에 선수 과목이 있다면 그 선수 과목부터 수강해야 하므로, 특정 과목들을 수강해야 할 때 위상 정렬을 통해 올바른 수강 순서를 찾아낼 수 있습니다. 이와 같이 선후 관계가 정의된 그래프 구조 상에서 선후 관계에 따라 정렬하기 위해 위상정렬을 이용할 수 있습니다. 정렬의 순서는 유향 그래프의 구조에 따라 여러개의 종류가 나올 수 있습니다. 위상 정렬이 성립하기 위해서는 반드시 그래프의 순환이 존재하지 않아야합니다. 즉, 그래프가 비순환 유향 그래프(directed acyclic graph:DAG)여야 합니다.
일반적인 위상 정렬의 적용은 주로 업무의 일정을 일어나야 할 순서에 따라 배치하기 위하는 것으로, 이 알고리즘은 프로젝트 관리 기법을 평가 및 분석하기 위한 기법(PERT)에 적용하기 위한 목적을 위해 1960년대 초반부터 연구되었습니다. 이 때, 해당 업무는 꼭지점으로 표현되었고, 각 꼭짓점을 연결하는 변은 해당 업무 간의 선후 관계를 표현하였습니다. 가령, 옷을 다리기 위한 업무는 반드시 옷을 세탁기에 돌리는 업무 뒤에 배치되어야 한다. 이와 같이, 위상정렬은 각 업무를 수행하기 위한 순서를 제공하였습니다.
위상정렬의 수행과정
BFS로 구현
- 자기 자신을 가리키는 변이 없는 꼭지점을 찾습니다.(진입 차수가 0인 정점(즉, 들어오는 간선의 수가 0인 꼭지점을 선택)
- 진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방합니다.
- 초기에 간선의 수가 0인 모든 정점을 큐에 삽입합니다.
- 찾은 꼭짓점을 출력하고 출력한 꼭짓점과 그 꼭짓점에서 출발하는 변을 삭제합니다.
- 선택된 정점을 큐에서 삭제합니다.
- 선택된 정점에 부속된 모든 간선에 대해 간선의 수를 감소시킵니다.
- 아직 그래프에 꼭짓점이 남아있으면 단계 1로 돌아가고, 아니면 알고리즘을 종료시킵니다.
- 위상 정렬의 과정에서 그래프에 남아 있는 정점 중에 진입 차수가 0인 정점이 없다면, 위상 정렬 알고리즘은 중단되고 이러한 그래프로 표현된 문제는 실행이 불가능한 문제가 됩니다.
구현 코드

두가지 구현방식이 있음 BFS, DFS, 우선순위 큐
위상정렬의 특징
출처 : https://ko.wikipedia.org/wiki/%EC%9C%84%EC%83%81%EC%A0%95%EB%A0%AC