티스토리 뷰
##제가 공부하면서 쓴거라 오류가 있을 수 있습니다
분산분석(변량분석)이란?
변량분석은 둘 이상의 집단 간 평균 점수를 비교하고자 할 때 실시하는 분석방법입니다. 차이검증(T검정)으로는 두 집단 끼리만 비교할 수 있지만 변량 분석을 이용하면 더 많은 집단 끼리도 비교할 수 있습니다. 평균의 차이검증
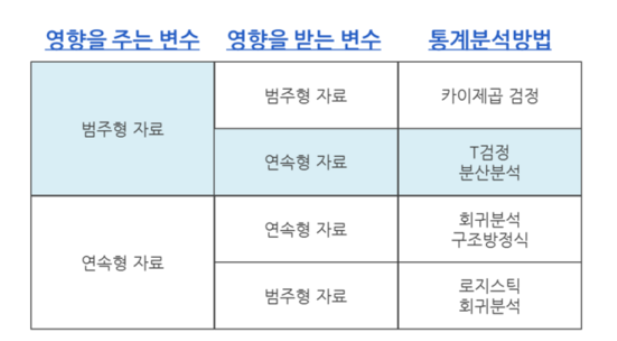
분산분석은 (영향을 주는 변수 : 범주형자료, 영향을 받는 변수 : 연속형 자료) 일때 적절한 통계적 분석 방법입니다.
범주형 자료의 집단이 두개일 경우 T검정, 범주형 자료의 집단이 세개 이상일 경우 분삭분석을 실시합니다.
일원배치 분산분석을 하기 위해서는 3가지의 조건이 부합되어야합니다.
정규성
각 모집단의 분포가 정규분포여야 합니다.
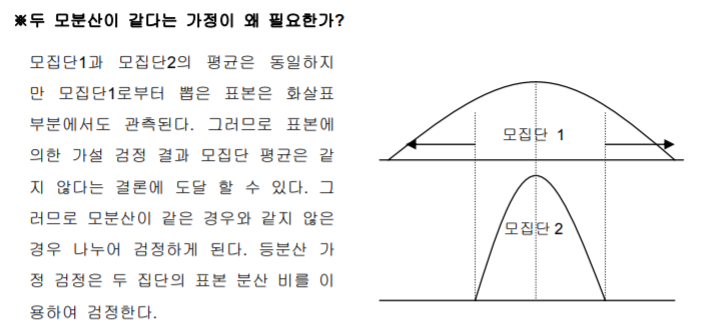
등(동)분산성
각 모집단 간의 분산이 동일해야 합니다.
독립성
각 모집단 간의 오차는 서로 독립이여야 합니다. 그리고 Completely Randomized Design(CRD)로 이우러져야 합니다.(각각의 run들을 대상으로) The environment is as uniform as possible for all experimental units. 즉, 실험의 실행은 랜덤하게 이루어져야 합니다.
다음으로 basic single-factor ANOVA model의 설명입니다.

여기서 iid란 independent and identically distributed의 약자입니다. 한국어로는 독립 동일 분포라고 합니다. a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent.
요약하자면 i.i.d.는 어떠한 랜덤 확률변수의 집합이 있을때 각각의 랜덤 확률변수들은 독립적이면서 (자기 사건의 발생의 영향이 다른 랜덤 확률변수에게 미치지 않을 때) 동일한 분포를 가질때를 의미합니다.
예를들어서, 이항확률 분포 (성공 or 실패)를 가지는 동전던지기를 3회 실시한다고 가정하면
각각의 시행은 이전이나 이후의 시행에 영향을 주지않는 독립시행이며 각각의 시행에서 나오는 동전의 앞,뒤에 대한 결과값의 분포는 동일한 이항확률 분포를 따르기 때문에 이는 i.i.d.라고 할수 있다.
all other source of variability in the experiment(measurement, uncontrolled factors, background noise) 는 입실론 ij에 대해 설명하고 있습니다. 그리고 모 분산은 상수로 가정하고 있습니다. 분산 분석의 특징 중 하나인 등분산성을 맞춰야하기 때문입니다.(확인필요)

또한 일원배치 분산분석은 두가지로 분류될 수 있습니다. Fixed effects model과 Random effects model입니다.
먼저 Fixed effects model에 대해 설명하도록 하겠습니다. 예를 들면, Fixed는 160, 180, 200, 220 이렇게 정해진 것에 대해서 실험하지만, Random은 160 ~ 220 중에서 random하게 하나를 고릅니다. 여기서 타우i를 fixed로 두냐 random으로 두냐에 따라서 yij의 평균과 분산이 달라지므로 꼭 구별하고 확인해야 합니다.

Fixed effect는 level이 무작위가 아닌 절차에 의해 선택되거나, 전체 모집단에서 가능한 수준(levels)으로 구성되는 factor입니다.
모든 관심 수준(levels)은 데이터셋에 있습니다. 연구자는 연구에 포함된 수준(levels)의 응답변수에 대해서만 factor의 효과(effects of factors)를 비교하는데에 관심이 있습니다. Fixed effect만을 포함하는 모형을 fixed effects model이라고 합니다. treatment를 선택하였기 때문에 parameter로 취급합니다. random distribution이 아닙니다.

시그마 i =1 에서 a까지 타우i를 더하면 0이 됩니다. fixed effect model 일때의 제약 조건입니다. 즉, 처리의 의한 변동은 없다고 하는 것이 constraint(제약조건)입니다.
더 자세히 정리해보겠습니다.


u + 타우i를 ui로 하는 것도 가능합니다.

귀무가설과 대립가설의 설명도 나와있습니다.

다음으로 random effects model입니다.
여기서 타우i가 random variables인 것을 주목합니다.

뮤가 parameter(constant)인 것에 주목한다.(확인필요) 또한 입실론ij에서 표준편차는 시그마i 하지만 분산은 같다고 했다. i가 달라도 표준편차가 다르지 않다. 또한 타우i의 분포에 주목하자 Fixed와 다르다. fixed에서는 입실론 ij만 iid였지만 random에서는 타우i도 iid이다.



예제입니다. a(처리,treatments) = 3이며, 반복 횟수는 n = 2입니다. 각 y와 공분산의 관계도 입니다. (Random effect model입니다.)

fixed effect model에 대해 더 자세히 알아보도록 하겠습니다. 귀무가설은 각 처리간의 변동이 없다고 주장하며, 대립가설은 적어도 하나는 0이 아니라고 주장합니다.

이러한 가정들은 analysis of variance(ANOVA)에 의해 테스트 됩니다. SST = 전체 변동


CT = collective total

집단내 자유도가 an-a(=a(n-1))인 이유 : 각 gropu에 대한 자유도는 n-1입니다. 그러므로 a개의 treatment에 대한 자유도는
a * (n-1)로써, 전체 표본의 갯수에서 treatment의 갯수를 뺀 결과로 보입니다( an - a)


yi.bar 와 y..bar는 정규분포 합니다.


귀무가설이 사실이면 F비율은 1에 가까워 지고, 대립가설이 사실이면 1보다 커지게 됩니다. 즉, 처리들 간의 변동이 군내 변동보다 우세하므로 처리간의 효과가 다르다는 주장을 할 수있습니다. F(a-1, an-a), a-1은 MStreatment에 대한 자유도, an-a는 MSe에 대한 자유도입니다. F비율이 1보다 작으면 MSe가 더 크므로 within variation이 between variation보다 더큰것을 확인할 수 있습니다.


위에서도 나온 표이지만 다시 정리하였습니다. 중요한 것은 F0은 귀무가설을 따릅니다.

예시입니다. 총 변동(SST) 계산시 전체 표본의 제곱과 전체 총합 제곱의 평균을 따로 계산하여 구하였습니다. 표가 주어질 경우 하나씩 계산하는것 보다 주어진 것을 활용하는 게 더 빠릅니다. 문제 풀이시 표를 주어주고 계산하는 문제가 있을 수 있으므로 형식에 익숙해지도록 합니다. 또한 SST와 SSt를 구하는 공식은 머릿속에 외워 두어야합니다.

위 그림을 보면 F비율의 값이 66.80으로 1의 값과 많이 떨어져 있는 것을 확인할 수 있습니다. 그러므로 Treatment간의 유의미한 차이를 가지고 있다고 볼 수 있습니다. 따라서 귀무가설을 기각하고 대립가설을 채택합니다. (p- value를 비교해봐야 합니다. 이것만 가지고 귀무가설을 기각 할 수 없습니다)