티스토리 뷰
출처 : https://www.acmicpc.net/blog/view/9
배열 A가 있고, 여기서 다음과 같은 두 연산을 수행해야하는 문제를 생각해봅시다.
- 구간 l, r (l ≤ r)이 주어졌을 때, A[l] + A[l+1] + ... + A[r-1] + A[r]을 구해서 출력하기
- i번째 수를 v로 바꾸기. A[i] = v
수행해야하는 연산은 최대 M번입니다.
세그먼트 트리나 다른 방법을 사용하지 않고 문제를 푼다면, 1번 연산을 수행하는데 O(N), 2번 연산을 수행하는데 O(1)이 걸리게 됩니다. 총 시간 복잡도는 O(NM) + O(M) = O(NM)이 나오게 됩니다.
2번 연산이 없다고 생각해봅시다.
수를 바꾸는 경우가 없기 때문에, 합도 변하지 않습니다. 따라서, 앞에서부터 차례대로 합을 구해놓는 방식으로 문제를 풀 수 있습니다.
S[i] = A[1] + ... + A[i] 라고 했을 때, i~j까지 합은 S[j] - S[i-1]이 됩니다.
i~j까지 합은 A[i] + ... + A[j]인데, S[j] = A[1] + ... + A[j], S[i-1]= A[1] + ... + A[i-1] 이기 때문입니다.
S[0] = A[0]; for (int i=1; i<n; i++) { S[i] = S[i-1] + A[i]; }
여기서 2번 연산을 하려면, 수가 바뀔때마다 S를 변경해줘야 합니다. 가장 앞에 있는 0번째 수가 바뀐 경우에는 모든 S 배열을 변경해야 하기 때문에, 시간복잡도는 O(N)이 걸리게 됩니다.
따라서, M과 N이 매우 큰 경우에는 시간이 너무 오래걸리게됩니다.
세그먼트 트리
세그먼트 트리를 이용하면, 1번 연산을 O(lgN), 2번 연산도 O(lgN)만에 수행할 수 있습니다.
세그먼트 트리의 리프 노드와 리프 노드가 아닌 다른 노드는 다음과 같은 의미를 가집니다.
- 리프 노드: 배열의 그 수 자체
- 다른 노드: 왼쪽 자식과 오른쪽 자식의 합을 저장함
어떤 노드의 번호가 x일때, 왼쪽 자식의 번호는 2*x, 오른쪽 자식의 번호는 2*x+1이 됩니다.
N = 10인 경우에 세그먼트 트리는 다음과 같습니다.

위의 그림은 각 노드가 저장하고 있는 합의 범위를 나타낸 그림입니다. 여기에 각 노드의 번호를 그림으로 나타내면 다음과 같습니다.

만들기
만약, N이 2의 제곱꼴인 경우에는 Full Binary Tree 입니다. 또, 그 때 높이는 logN 입니다. 리프 노드가 N개인 Full Binary Tree는 필요한 노드의 개수가 2*N-1개 입니다.
N이 2의 제곱꼴이 아닌 경우에는 높이가 H = ⌈lgN⌉ 이고, 총 세그먼트 트리를 만드는데 필요한 배열의 크기는 2^(H+1) - 1개가 됩니다.
다음과 같은 과정을 거쳐서 Segment Tree를 만들 수 있습니다.
// a: 배열 a
// tree: 세그먼트 트리
// node: 세그먼트 트리 노드 번호
// node가 담당하는 합의 범위가 start ~ end
long long init(vector<long long> &a, vector<long long> &tree, int node, int start, int end) {
//leaf node
if (start == end) {
return tree[node] = a[start];
} else {
return tree[node] = init(a, tree, node*2, start, (start+end)/2)
+ init(a, tree, node*2+1, (start+end)/2+1, end);
}
}
start == end 인 경우는 node가 리프 노드인 경우입니다. 리프 노드는 배열의 그 원소를 가져야 하기 때문에 tree[node] = a[start]가 됩니다.
node 의 왼쪽 자식은 node*2, 오른쪽 자식은 node*2+1이 됩니다. 또, node가 담당하는 구간이 [start,end] 라면 왼쪽 자식은 [start,(start+end)/2], 오른쪽 자식은 [(start+end)/2+1,end]를 담당해야 합니다. 따라서, 재귀 함수를 이용해서 왼쪽 자식과 오른쪽 자식 트리를 만들고, 그 합을 저장해야 합니다.
합 찾기
구간 left, right이 주어졌을 때, 합을 찾으려면 루트부터 트리를 순회하면서 각 노드가 담당하는 구간과 left, right 사이의 관계를 살펴봐야 합니다.
예를 들어, 0~9까지 합을 구하는 경우는 루트 노드 하나만으로 합을 알 수 있습니다.

2~4까지 합을 구하는 경우는 다음과 같습니다.
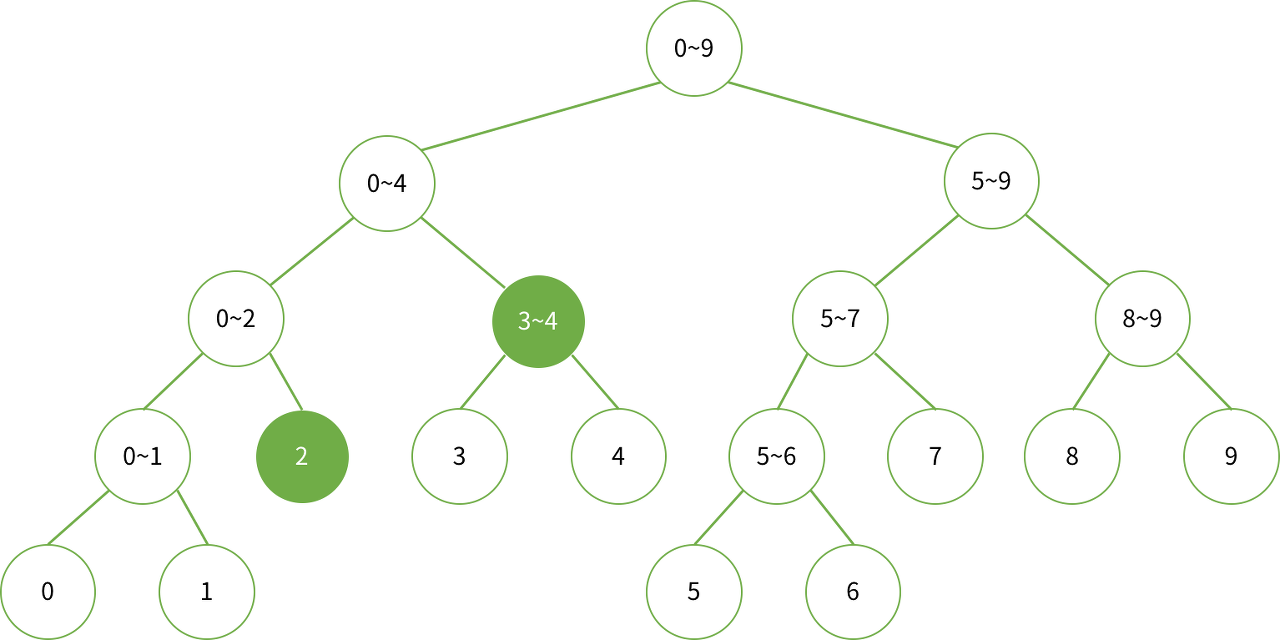
5~8까지 합을 구하는 경우는 다음과 같습니다.

3~9까지 합을 구하는 경우는 다음과 같습니다.

node가 담당하고 있는 구간이 [start,end] 이고, 합을 구해야하는 구간이 [left,right] 이라면 다음과 같이 4가지 경우로 나누어질 수 있습니다.
- [left,right]와 [start,end]가 겹치지 않는 경우
- [left,right]가 [start,end]를 완전히 포함하는 경우
- [start,end]가 [left,right]를 완전히 포함하는 경우
- [left,right]와 [start,end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우)
1번 경우에는 if (left > end || right < start)로 나타낼 수 있습니다. left > end는 [start,end] 뒤에 [left,right]가 있는 경우이고, right < start는 [start,end] 앞에 [left,right]가 있는 경우입니다. 이 경우에는 겹치지 않기 때문에, 더 이상 탐색을 이어나갈 필요가 없습니다. 따라서 0을 리턴해 탐색을 종료합니다.
2번 경우는 if (left <= start && end <= right)로 나타낼 수 있습니다. 이 경우도 더 이상 탐색을 이어나갈 필요가 없습니다. 구해야하는 합의 범위는 [left,right]인데, [start,end]는 그 범위에 모두 포함되고, 그 node의 자식도 모두 포함되기 때문에 더 이상 호출을 하는 것은 비효율적입니다. 따라서, tree[node]를 리턴해 탐색을 종료합니다.
3번과 4번의 경우에는 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 시작해야 합니다.
// node가 담당하는 구간이 start~end이고, 구해야하는 합의 범위는 left~right
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right) {
//1번 경우
if (left > end || right < start) {
return 0;
}
//2번 경우
if (left <= start && end <= right) {
return tree[node];
}
return sum(tree, node*2, start, (start+end)/2, left, right)
+ sum(tree, node*2+1, (start+end)/2+1, end, left, right);
}
수 변경하기
중간에 어떤 수를 변경한다면, 그 숫자가 포함된 구간을 담당하는 노드를 모두 변경해줘야 합니다.
다음은 3번째 수를 변경할 때, 변경해야 하는 구간을 나타냅니다.

다음 그림은 5를 변경할 때입니다.

index번째 수를 val로 변경한다면, 그 수가 얼마만큼 변했는지를 알아야 합니다. 이 수를 diff라고 하면, diff = val - a[index]로 쉽게 구할 수 있습니다.
수 변경은 2가지 경우가 있습니다.
- [start,end]에 index가 포함되는 경우
- [start,end]에 index가 포함되지 않는 경우
node의 구간에 포함되는 경우에는 diff만큼 증가시켜 합을 변경해 줄 수 있습니다. tree[node] = tree[node] + diff 포함되지 않는 경우는 그 자식도 index가 포함되지 않기 때문에, 탐색을 중단해야 합니다.
void update(vector<long long> &tree, int node, int start, int end, int index, long long diff) {
//index가 구간에 포함되지 않은 경우
if (index < start || index > end) return;
//index가 구간에 포함된 경우
//내려가면서 거치는 모든 노드들을 변경해야 한다. 리프노드가 아닐경우, 내려가면서 변경분만 더하면 되고
tree[node] = tree[node] + diff;
//리프노드에선 더이상 내려가지 않는다
if (start != end) {
update(tree,node*2, start, (start+end)/2, index, diff);
update(tree,node*2+1, (start+end)/2+1, end, index, diff);
}
}
리프 노드가 아닌 경우에는 자식도 변경해줘야 하기 때문에, start != end로 리프 노드인지 검사를 해야 합니다.
세그먼트 트리를 이용해서 2042번 문제: 구간 합 구하기 번을 풀 수 있습니다. 최소값, 최대값도 합을 구하는 세그먼트 트리를 응용해서 구현할 수 있습니다. 10868번 문제: 최솟값, 2357번 문제: 최솟값과 최댓값